Math Motivation is the Key to STEM Career Success

Related Topics:

Psychological Principles of Learning re: Piaget

One goal of math educators has to be to see that the motivation to do maths survives through high school. Why? It is because without that students will not have the opportunity to go to University to take courses in STEM occupations. That's Science, Technology, Engineering and Mathematics: STEM. That's right, without grade 12math, your child is not going to be a doctor, lawyer, scientist, engineer, x-ray tech, optometrist, architect, etc. See Top 300 Highest-Paying Careers for a list of best paid careers. 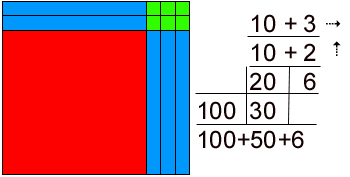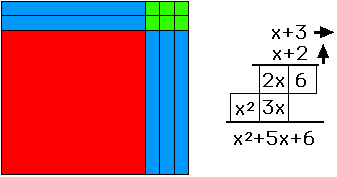With possible exception of CEO, Art Director, Film Director, Occupational Therapists, and Pro Sports, there are no top-paying jobs without grade 12 math. And we certainly hope CEOs know enough about math: inflation, profits & loss, etc. to run the companies our pensions are invested in. So, how do we ensure motivation survives grade 10 when they often get the choice to drop math 30 and take some watered-down course designed to help them feel good because they passed something? How? Easy, make it comprehensible, make it sensorial, make it visual. Make it appropriate to the natural cognitive development of a healthy child. Piaget informs us that no child can have the mental capacity to deal with abstract symbols and concepts before they have had the necessary tactile motor-kinesthetic, and concrete experiences to build a mental framework to deal with abstractions. In simpler language, a child cannot solve abstract problems without the relevant concrete experience of the world. You have to know that water is wet, and heavy before you can design a dam, and you discover this in a sandbox in kindergarten. You've got to play with the blocks to develop a visceral understanding of number. Otherwise it is just rote-memorization of facts, rules, formula and process. That may get you through elementary and junior high school but it cannot lead to the understanding of concepts needed to solve advanced story problems. That needs more than just memorizing times-tables and a few formulae. The test scores will show this. Worse, those who labored diligently studying for hours and hours to memorize enough to pass the exam will often drop math, never wanting to do anything like that again. So, what was the point? If we can coax and cajole, bribe and threaten students enough to pass grade 12 math only to see them drop it and take a non-math job paying low wages, did we fail them? I think so. It is not necessary. Fortunately, thanks to Maria Montessori, Jean Piaget and Jerry Mortensen kids don't have to hate math and ultimately drop it to get done with the stress. The answer to how we get motivation that survives grade 10 and 12 enabling possible futures in STEM and other high-paying careers is this: success. Nothing succeeds like success. Create learning situations where success is not only possible, but inevitable. Use the skills the child already has to teach math, instead of forcing them to depend on unreliable short-term memory for success. Play, or rather activities that yield tactile motor-kinaesthetic- experiences on which pre-concepts may be built is the key to success. They provide the mental framework on which concepts may be constructed, assimilated and accommodated - to use Piagetian terms. Put out the blocks. The Teacher's Handbook, shown at right and below, will show you how to use the manipulatives and Mortensen concepts in an easy, visual manner. Encourage play. Practice counting them. Build rectangles. Ask questions. Draw them. Visualize them. Tell stories with them. Use the blocks in every example until seeing them instead of symbols, or along with symbols becomes intuitive. See all numbers as rectangles. All we do in math is count. The point here is to teach counting in concrete terms, rather than with symbols. Piaget has shown that it is pointless to employ abstract teaching concepts before the mind is ready but we can still teach the skills of mathematics. we can teach "kindergarten calculus." All we do in math is count.

So what do you need to start teaching math the Mortensen way? The Handbook for Teaching Math with Manipulatives is 250 large pages of detailed, illustrated, easy-to-read instruction in employing the Mortensen method written by Canada's leading practitioner of the method. Delivered to you in PDF, it prints to 8.5 by 11 inch format. Included are 200 pages of actual lessons on all topics from whole number operations to fractions to functions! Never be without a lesson again! Every lesson/example is fully illustrated. After all, this is a visual approach. Key phrases in simple language are highlighted, giving the preferred verbalizations to transmit important math concepts. Actual student responses give experienced teachers the right track to run-on. A consistent approach gives clarity to the pattern employed with all examples in the curriculum. Every example includes the steps of Build it with manipulatives, Draw it to develop Visualization, do the Notation, and Record the answer. Specific lessons on teaching Notation, e.g. algorithms for operations, occur throughout. Also a chapter on the teaching of algorithms of notation and the significance of the relationship between them and the spatial reality of the constructions is included. The psychology of employing manipulatives is explained. In particular the value of the tactile motor-kinaesthetic experiences to learning mathematics is discussed. To Order: The Teacher's Handbook for Teaching Math with Manipulatives by Geoff White, B.Ed. Send $65 by Paypal to geoff @ geoffwhite.ws NB. no spaces in the e-mail addresses Delivery by e-mail is same day if M-F office hours