An example with Fractions

Mortensen Math has the advantage that it is comprehensive, that is, its principles apply across all topics: arithmetic (including decimals and fractions), measurement, algebra, calculus, problem solving, etc. In addition, it is universal, that is, the same principles and method are used in all topics, so the student can transfer the skills learned in say, multiplying whole numbers to multiplying fractions and polynomials. This makes comprehension quicker and more satisfying than having to learn many different techniques and rules.

Consider your query for example, doing two-digit multiplication with whole numbers in the traditional way involves knowing multiplication facts (times tables) and the algorithm (placing the two numbers atop one another, lining up units and tens, then applying the rules of operation.) This is very different from multiplying fractions! - which relies on knowing the rule: "multiply top times top, bottom times bottom, reduce to lowest terms, record the answer," and that bears no resemblance to the other.

The traditional algorithm for two-digit multiplication looks like this:

   12
  x13
   36
  12 
 156 

And looks nothing like the notation for multiplying fractions: 1/2 x 1/3 = 1/6

In MM, because manipulatives are used, the construction looks identical when multiplying whole numbers or fractions, therefore the child can see the similarity, can apply the skills learned while doing whole numbers to the fractions, and be much happier and more successful.

In MM, we build the example with the blocks, then draw it, then do the notation, then record the answer. This provides two more parts to the learning than is traditionally done in public schools. These two parts are critical because they provide hands-on experiences, and reinforcement by visualization. Thus in MM, the whole number multiplication looks like the drawing below,

eg.

The quantity, represented by an area on the top surface of the blocks, is "13 over" and "12 up." Count up the blocks and you will see, one hundred, five tens (or fifty), and six. One hundred fifty-six.

Similarly with fractions, multiplication examples ask, How much (area) is 1/2 times 1/3? It is an area 1/2 over and 1/3 up. We can use combo blocks or plastic overlays to construct the example. Then we would draw it. One is a rectangle that measures one unit over, one unit up. It is a square. Go over one half, then go up one third and see the rectangle that describes. See below:

eg.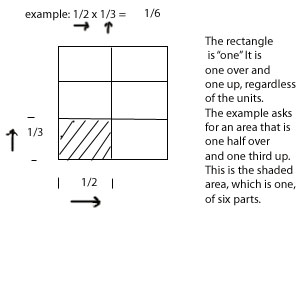

---

A Division Example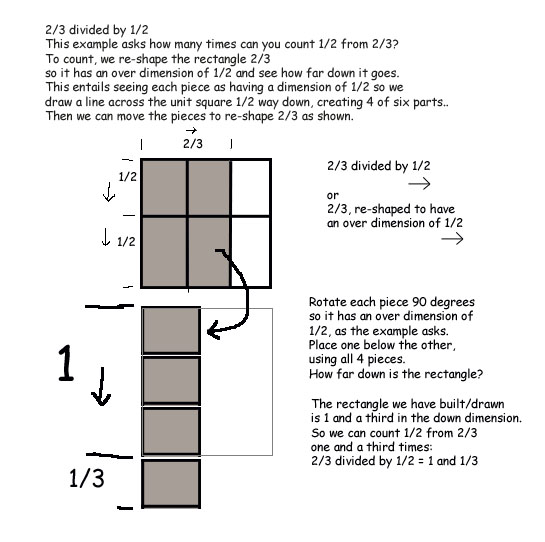

The chapter on teaching fractions with manipulatives using the MM method from my Teacher's Handbook is available by itself for $20 (in .pdf, no postage!) It is fully illustrated and covers all operations with fractions using two different kinds of manipulatives: blocks and overlays, but you can substitute drawing for the overlays quite easily.

Or, you can have the whole Teacher's Handbook that covers all the topics K-12 for $65 in .pdf As soon as I receive payment by Paypal, I ship right away. You get it by email the same day! (M-F, 10-5)

Paypal only please.