Teaching Math With Manipulatives

By 3yrs old Suzy has learned a foreign language (she wasn't born with one) without formal training or a textbook. Why? Because she lives in a language-rich environment.

Her home is filled with books, magazines, her parents read by themselves as well as reading bedtime stories to her. She visits the library where she discovers a whole world of books and language, even different languages. The radio is playing at different times and on it people are talking throughout the day. Her parents put the TV on for the news at 6pm. She hears people talking with her parents when they visit, when they go shopping or to the park.

In a math-rich environment, she would be exposed to stimuli for all of the senses. If alphabet soup encourages us to like letters, then number cookies should encourage us to like math. Also, pictures of Pyramids and Fibonacci spirals, may adorn the walls or bulletin boards, fridge magnets of different shapes may be seen, and played with. Her parents may play music: Bach fugues, skip-counting songs & other rhythms, may be heard. Aromas: Chanel No.5? and of course, manipulatives will be present in her surroundings. Blocks for building, shapes for making designs, snowflakes, stars, squares and rectangles, as well as circles. Origami mobiles can be hung for decoration. There are many possibilities for filling the living space with interesting examples of math in action. Developing awareness is key in developing interest.

It is important that these math examples be interactive too. Static displays hold interest only briefly. Play is the means by which we become familiar with our world. A child should be enabled to explore and discover her environment.

Playing in the kitchen sink with measuring cups, pots and cups of different sizes is a wonderful activity. Cooking and baking require measurement and the results are significant when taste is involved.

Consider for a moment the opposite: an environment void of number. What can we know of our world if we cannot, do not count and measure it? How far is it to the store? The beach? The park? Grandma�s house? Which house do we live in? What street? Do we have a post box? How big is our lot? How many steps is it to the roadway? How many floors does the house have? Our apartment have? And so on.

We may describe our world in words, but to examine it we employ numbers. Let�s get started.

Because understanding a concept is usually accompanied by the production of dopamine and endorphins in the brain, in short, pleasure, when that little light goes on, and you finally "get it," it feels good!

Jean Piaget and Maria Montessori have shown that understanding of concepts occurs naturally in children if the appropriate sensori-motor experiences can be had. That means the necessary opportunity for exploring and discovering concepts must be provided for the children to learn naturally; in other words, play.

But not just any play, if you want children to learn language you must provide a language-rich environment. If you want children to learn math concepts you must provide a math-rich environment. More on that later, let's get this straight: sensori-motor experiences of the right kind are necessary for the acquisition of schemas - groups of experiences, that can be assimilated and synthesized into concepts or accommodated by the child's mind. This sense of understanding is enjoyable and is all that is needed for successful learning.

It is our mission as teachers and parents to provide the appropriate materials and situations for this to happen, and sometimes just to get out of the way.

By 1998 the demand on my schedule had become so heavy I knew had to find another way to reach more people. My solution was to record my workshop on video. I willingly sent the tapes to interested parties I couldn't teach in person. The problem with that scheduling solution was no one could ask questions. Extra explanations were missing because I wasn't there in person at the white board. That led me to the development of a handbook.

I'll tell you more about that in a minute. You probably want to know more about the Mortensen Math system first.

MORTENSON MORE THAN MATH employs manipulatives, such as the red, blue, and green ones at right and below, to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality.

The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you?

Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well.

The truth is the entire math curriculum used in traditional teaching situations such as public schools,
relies on memorizing FACTS, RULES, FORMULAE AND PROCESS!

Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the Mortensen method does. Take for example 13 x 12 = ? Visualize the numbers as rectangles using the tiles above and you get this:
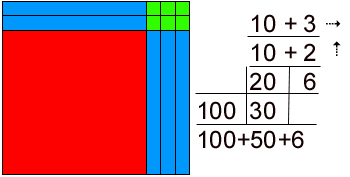Since the answer is a number, if you visualize numbers as rectangles, then all operations in math are just building rectangles. All we do in math is count, and, building rectangles makes the counting easier and more accurate.

What I just did was to make math visual, tactile and easily understandable by using a multi-sensory approach. Math just became play. How fun is that!

Order The Teacher's Handbook
for Teaching Math with Manipulatives
Only US$65, by Paypal to

geoff @ geoffwhite.ws (no spaces)

| Purchasing Dilemmas | Products/Price List | Comparing Methods | Understanding | Mental Images | A Fractions Example | Psychological Principles at Work | Self-Esteem - Teacher's Role | Acquiring Meaning | A Philosophy of Teaching Math | Main Page