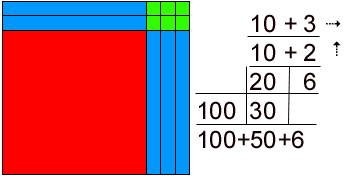
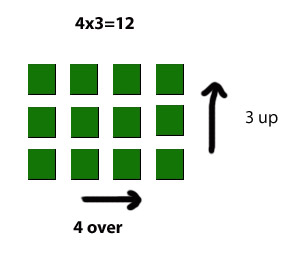
In Mortensen Math we construct models of various problems. At the same time we create mental images of those problems. The content of these images is visual, eg. (fig. at right)
|
In Philosophy of mind there have been objections raised regarding the existence of mental images by Dan Dennett, Saul Kripke and others. The question is asked, "What are these mental images like? Do you have a little screen and a movie projector running in your head? If you have a mental image of a tiger, tell me how many stripes has he got?" If you cannot say how many stripes the tiger has, is this meant to be some kind of fatal objection to the concept of mental images? Supposedly, if you cannot meet the standards imposed by actual photographs then mental images must not actually exist, even when hundreds of millions of human beings will attest to their reality, and, in fact, use mental images every day just to survive. But it seems to me that is not the right sort of question to ask about mental images. The evolutionary advantage gained by having mental images that has enabled the possessor of this ability to have progeny that survive today to demonstrate the ability, is to extract the relevant information from their mental images. To put it more strongly, the human who could extract critical information from his mental image of a tiger, survived! The tiger has superior size, speed, claws, huge jaws and killer teeth. The number and variety of its stripes are irrelevant. Those humans who had the ability to count the stripes probably got eaten and do not survive today to be able to answer Dennett's question. In MM we want students to be able to extract the critical information. This is made easier by using manipulatives of primary colors, - bright, vivid, easily recognizable colors: a red square a blue bar and a green cube, as well as colored pieces from two to nine. The abilities we are training, include: recognizing shapes - squares and rectangles, identifying sizes: units, tens, hundreds, recognizing "completeness" eg. a hole in the construction, or an extra bit sticking out. These are all visual data and form vivid mental images which are easily remembered, more so than say, the product of six times six - if the answer is merely a pair of symbols: "3" and "6." If you try to "see" all numbers as rectangles, then 12 becomes a rectangle that is 4 over and 3 up - sometimes.
It can easily be re-shaped if the problem calls for it.
The critical features of the mental images useful in MM are: shape, size, color and completeness. These features depend on visual and tactile clues which are easily assimilated through the use of manipulatives. Build it. Draw it. Do the notation. Record the answer. By 1998, the demand on my schedule had become so heavy I knew had to find another way to reach more people. My solution was to record my workshop on video. I willingly send the tapes to interested parties I couldn't teach in person. The problem with that scheduling solution was no one could ask questions. Extra explanations were missing because I wasn't there in person at the white board. That led me to the development of a handbook. I'll tell you more about that in a minute. You probably want to know more about the Mortensen Math system first. MORTENSON MORE THAN MATH employs manipulatives to enhance the child's ability to visualize math concepts, to decode the mathematical language into spatial reality. The best way I know to explain the Mortensen Math system is to talk about memory first. How good is your short-term memory? More importantly, how good is your short-term memory with numbers? Suppose I gave you 12 numbers, each of them seven digits long. Do you think you could remember them for an hour? Five minutes? Do you think you could remember them long enough to write them down, even right after I told you? Not likely. That's because you've been taught like everyone else to memorize the hard way. The hard way is how most students are taught math as well. The truth is the entire math curriculum used in traditional teaching situations, employing textbooks, relies wholly on memorizing nothing but FACTS, RULES, FORMULAE AND PROCESS! Now consider an infant - no tutors, no special training, yet soon after opening her eyes she can remember Mom's face and can pick her out from a sea of relatives gawking into the cradle. Why? Because visual memory is the most powerful. From one glance we can perceive huge amounts of information and retain it indefinitely, extracting detail months, even years later. Tell me, which hand does Lady Liberty hold aloft? What is she holding in that hand? What is tucked under her other arm? How long did you spend studying the Statue of Liberty before I asked? Our job as educators is to decode this mathematical language of symbols into a concrete reality. This is what the method does.
|


So what do you need to start teaching math the Mortensen way?
The Handbook for Teaching Math with Manipulatives is 250 large pages of detailed, illustrated, easy-to-read instruction in employing the Mortensen method written by Canada's leading practitioner of the method. Delivered to you in PDF, it prints to 8.5 by 11 inch format. Included are 200 pages of actual lessons on all topics from whole number operations to fractions to functions! Never be without a lesson again! Every lesson/example is fully illustrated. After all, this is a visual approach.
Key phrases in simple language are highlighted, giving the preferred verbalizations to transmit important math concepts. Actual student responses give experienced teachers the right track to run-on. A consistent approach gives clarity to the pattern employed with all examples in the curriculum. Every example includes the steps of Build it with manipulatives, Draw it to develop Visualization, do the Notation, and Record the answer. Specific lessons on teaching Notation, e.g. algorithms for operations, occur throughout. Also a chapter on the teaching of algorithms of notation and the significance of the relationship between them and the spatial reality of the constructions is included. The psychology of employing manipulatives is explained. In particular the value of the tactile motor-kinaesthetic experiences to learning mathematics is discussed.

To Order:
The Teacher's Handbook for Teaching Math with Manipulatives
by Geoff White, B.Ed.
Send $65 by Paypal to
geoff @ geoffwhite.ws
NB. no spaces in the e-mail addresses
Be careful to include all the correct shipping details
Delivery by e-mail is same day if M-F office hours
| Purchasing Dilemmas | Products/Price List | Comparing Methods | Understanding | Mental Images | Math Motivation | A Fractions Example | Psychological Principles at Work | Self-Esteem - Teacher's Role | Acquiring Meaning | A Philosophy of Teaching Math | A Math-Rich Environment | Main Page