A Philosophy of Teaching Mathematics

Related Topics:

Psychological Principles of Learning re: Piaget

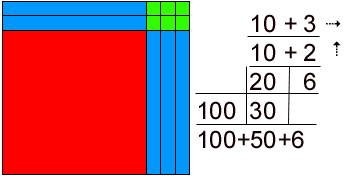
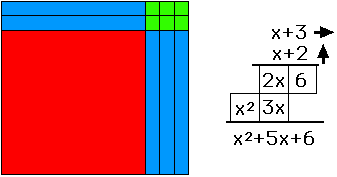
Where does the idea of a philosophy of mathematics come from? Some of the first questions we ask are: What is there? What can I Know? and What ought I to do? Often philosophy is seen not as a discipline that gives answers, but merely hopes to ask better questions. I have a goal in mind, and that is, to do away with an establishment that seeks to bury math in symbolism, literally full of Greek symbols such as pi and delta unfamiliar to almost everybody, to demystify the activities that hide behind unexplained processes, such as calculus and algebra, even long division, which have plagued students for more than a century, since the inception of public schools. What I mean to do is to decode this mathematical language into a spatial reality. After observing the world and the people and things in it we then want to talk about it. For this we employ language and the first task is to name things: mother, father, pig, tree, antelope, and so on. Then we might want to say something about the scope of the world - how big things are, how far away things are, how many things there are. We employ metaphor: The buffalo are as many as there are fish in the sea, or as John Cabot told his King of the fish on the Grand Banks: They are so plentiful a man could walk on their backs from Greenland to Nova Scotia. Primitive man had only a few numbers: one, two, three and many. This sufficed for a primitive life. It had survival value up to a point. As long as there was enough buffalo to eat who cares how many there actually are? Need dictates. When the metaphor breaks down we must resort to counting. To describe the world, to say what there is and how many there are, a few wavy hand gestures and holding up some fingers works up to a point. "Many buffalo, two days ride, that-a-way!" just about does it, until the population outnumbers the resources, then we need the accountants. To master bigger numbers than we have fingers for we employ symbols and right there we lose almost everybody. It is a common complaint to say, "I can't even balance my cheque book!" What happened at that point was that by employing symbols mathematics was removed from the world of the concrete into the abstract. This is not a necessary transformation. It has however been used to separate understanding from practice for most people and resulted in frustration, a sense of powerlessness and exploitation. How many big money earners have been defrauded by managers who knew more about manipulating numbers than their employers? If the math was concrete and available to everyone this wouldn't happen, at least, not so often. It may be that a fool and his money are still parted - eventually. What I said I wanted to do is to decode the mathematical language into a concrete reality. You see ( a key phrase) what has happened is that symbols are introduced into the learning process before the pre-pubertal mind can comprehend them, and rote and process learning has been substituted for understanding. Instead of understanding numbers, we merely train the processes of manipulating symbols according to rules and formula which must merely be remembered in lieu of understanding. recitation has taken the place of comprehension. This program has gone unchallenged for decades, for so long that most people think that there is no alternative, that children must be forced into the memorization of facts, rules, formulae and process, that that is all there is to math. Yet the alternative has been in front of us all along. To what am I referring? Why the very books we use to teach the subject. Open the schoolbooks. The storybooks, the atlases, the geography books about foreign lands and the people who live there, the history books about colonial North America, cook books for HomeEc, shop manuals for woodwork and car mechanics, science books about heat and light and sound. What do you see Pictures. You see a picture and a story below it, saying something about the picture. A picture is worth a thousand words. In the first storybooks we use to teach children there is only a picture of a thing, a boy, a dog, a ball, and the name printed underneath. this is the pattern. Open the math text, what do you see? Where are the pictures? What has happened as I said above is that we jumped straight to symbols, 6, +, -, x, etc. leaping from a vision of the world to abstract notation, bypassing the pictures altogether. This has made understanding impossible for almost all children. Piaget explained that the human goes through stages of development from sensori-motor to concrete operational to abstract which takes 10-14 years or more and no amount of coercion can change that. So in order to save children from counting on their fingers for ten years until their cognitive; development renders them capable of grasping abstract concepts, to give them something to do from grade one through grade ten we have resorted to drill and recitation, endless practice of meaningless skills so that when their intellect is ready for algebra, so the thinking goes, they can understand (suddenly) what we have been going on about for the first decade and a half of their lives. The cost in terms of their patience and cooperation has been enormous. Many children resent the boredom of mathematics the seemingly senseless waste of their time doing endless reams of sums for ten years that by the time they get to Grade 10, where there is often an option to drop math or at least to take some practical course like shop math or bookkeeping that may lead to employment is possible. That in a nutshell is the problem To put it in the form of a question, what is the point of training efficiency and competence in arithmetic for the first ten years of a child's life if the cost is that it puts them off ever wanting to do math again? If they can be persuaded to study, to memorize the facts, rules, formulae and process necessary to achieve competence in math for ten or twelve years of schooling, but at the end they just hope they can remember it long enough to pass the exam and hope they never have to do it again, what really was the point of doing math in the first place? The solution? Change the method of presenting and doing math from grade one or two say, up to grade 8 or 9 or 10. Grandma and the pre-school teachers and the grade one teachers are doing just fine. All a child needs to start with they are already getting: the ability to count to nine and to build a rectangle. Although we have something to say about the counting. If little Johnny can say, "one, two, three, four, five, six, seven, eight, nine, ten." Can he count? No. Well, maybe. You see all he has demonstrated is that he has memorized the names of he numbers, as he has memorized his A,B,Cs. But there is more to counting than knowing the names of the symbols 1,2,3,4,5,6,7,8,9, and 10. You have to know that 4 is larger than 3. If we assumed that the child would know that 4 was bigger than 3 because it came later in the sequence wouldn't he think that Z was 26 times bigger than A? All we know from the recitation is that he knows the names of the number symbols, just as he knows the names of the letter symbols. We need to teach to concept of magnitude and nothing is simpler than to substitute a manipulative, a plastic block, say, for the symbols, initially. Let us use a small cube, a little green block, attractive, non-threatening. Let us hold it up as the child holds his and say, "This is one." Then let us hold up a small orange block - merely so that it is easily distinguishable from the one by looking, and say, "This is two." The two-block will be the same size as two green "ones" placed together. Then let us hold up a pink block and say, "This is three." The pink block will be the same size as three ones placed together. And so on. We will lay them out on the table and say these are the numbers, one, two, three, etc. and we may write down the symbols below the blocks and say, "These are the names of the numbers." The point here is to teach counting in concrete terms, rather than with symbols. Piaget has shown that it is pointless to employ abstract teaching concepts before the mind is ready but we can still teach the skills of mathematics. we can teach "kindergarten calculus." All we do in math is count.

So what do you need to start teaching math the Mortensen way? The Handbook for Teaching Math with Manipulatives is 300 large pages of detailed, illustrated, easy-to-read instruction in employing the Mortensen method written by Canada's leading practitioner of the method. In an 8.5 by 11 inch format, it lays flat on the table for easy reference - no more spine-breaking stiff texts that need to be weighted down for hands-free use. Included are 200 pages of actual lessons on all topics from whole number operations to fractions to functions! Never be without a lesson again! Every lesson/example is fully illustrated. After all, this is a visual approach. An idealized Teacher-Pupil dialogue is included in all lessons. If only the students would learn their part in the script! Key phrases in simple language are highlighted, giving the preferred verbalizations to transmit important math concepts. Actual student responses give experienced teachers the right track to run-on. A consistent approach gives clarity to the pattern employed with all examples in the curriculum. Every example includes the steps of Build it with manipulatives, Draw it to develop Visualization, do the Notation, and Record the answer. Specific lessons on teaching Notation, e.g. algorithms for operations, occur throughout. Also a chapter on the teaching of algorithms of notation and the significance of the relationship between them and the spatial reality of the constructions is included. The psychology of employing manipulatives is explained. In particular the value of the tactile motor-kinaesthetic experiences to learning mathematics is discussed. Order The Teacher's Handbook for Teaching Mathematics with Manipulatives right now, and I will include a 5-hour VHS videotape of my workshop covering the entire Mortensen method using three different sets of manipulatives, at no extra charge! This videotape of my workshop, videotaped at the University of Calgary, is a $99 value by itself. But I'll include it FREE if you order within 30 days. Imagine being able to reference lessons from the curriculum, including: all operations, problem solving, decimals, algebra, fractions - and being able to watch the lesson being taught by "Canada's resident expert on Mortensen Math" at the same time! Special Offer! Purchase The Teacher's Handbook for Teaching Math with Manipulatives right away and receive a very special bonus! Multiplication Facts are an undeniable foundation stone to learning math and the most enjoyable way of acquiring them is by means of songs and music. This audio tape of Jerry Mortensen himself playing keyboards and singing ten skip counting songs, which accompany his specially designed coloring books - very popular with younger learners, is a $10 value and I'll send it FREE if I receive your order within 30 days. Yours sincerely, Geoff White, B.Ed. To Order: The Teacher's Handbook for Teaching Math with Manipulatives by Geoff White, B.Ed. Send $79 by Paypal to geoff @ geoffwhite.ws Be careful to include all the correct shipping details Order by Jan 31, 2012 and receive, FREE! the 5 hour VHS workshop videotape (a $99 value) and the Special audiotape of Jerry Mortensen performing Skip Count Songs! (a $10 value) Absolutely FREE! Act now! Shipping USA & Canada please include $20 S&H; for elsewhere, inquire please.