Teaching Math with Manipulatives

Notes re: Comparative Methods for CBC radio interview with Sheila Rogers, 2008

#1 Should we base our math teaching on the weakest mental skill children possess, or on the strongest?

Two quick questions: #1 Imagine the statue of Liberty. See the skyline of Manhattan? See her pointy crown and flowing robes? What is she holding in her right hand? What is tucked under her left arm? So, you can extract information from a visual image you didn't even study, fairly easily. Now.. #2 If I give you twenty ten-digit numbers, how long can you remember them? An hour? Ten Minutes? Long enough to write them down? Why would you base your teaching on children's weakest mental ability: short term memory, rather than say, imagination?

#2 The goal is to think creatively in problem solving, not the recitation of number facts.

Looking to the future: employers aren't interested in whether you can recite your times tables, they have computers to do that. They want people who can solve their problems and develop creative strategies to make them profitable.

#3 Rote memorization results in boredom not excitement, in de-motivation rather than motivation.

Your average ten-year-old boy would rather run outside and play baseball than memorize times tables, which has about as much meaning to him as reciting poetry in ancient Greek (think Homer).

#4 Understanding cannot arise naturally from mere memorization of abstract facts cf. John Searle, "Chinese Room"

A computer can exchange symbols rapidly in a literal translation of Chinese symbols into say, the Russian language. But it will never learn to speak Chinese this way, or Russian, for that matter.

#5 Concept formation results from relevant physical experiences appropriate to student's cognitive stage.

There is no logical way to reach understanding from the mere memorization of abstract symbols.

#6 After Jean Piaget, Swiss Psychologist, prior to age 14 approx., children need "tactile motor kinaesthetic" and "concrete operational" experiences, not practice in symbol manipulation.

#7 Without old school methods of discipline is memory training even possible?

How can you "make" children do anything they don't already want to do? At early ages, learning strategies must focus on "Play and Discover," acquiring experiences from which to generalize and form concepts.

#8 Motivation: What if we succeeded in coaxing, cajoling, training a student to math competency at Gr.12, but in so doing put them off pursuing math at a post-secondary level? Would it have been worth it?

Isn't that what is happening to a majority of students at present, with methods based on memorizing facts, rules, formulae and processes?

#9 National perspective: Math competence can be grown or it can be imported, but can Canada compete in the world economy without it?

Student Achievement in Mathematics - StatsCan

If learning math were fun how hard would it be to get the students to do their work?

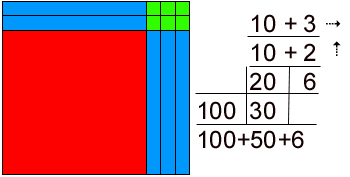
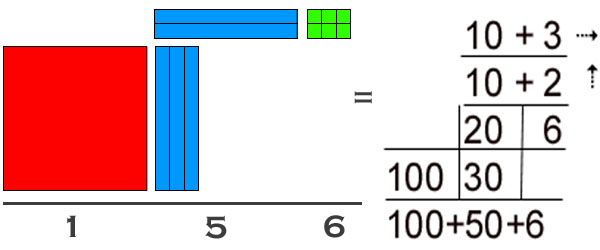
So what do you need to start teaching math the Mortensen way?

The Handbook for Teaching Math with Manipulatives is 250 large pages of detailed, illustrated, easy-to-read instruction in employing the Mortensen method written by Canada's leading practitioner of the method. In an 8.5 by 11 inch format, it lays flat on the table for easy reference - no more spine-breaking stiff texts that need to be weighted down for hands-free use. Included are 200 pages of actual lessons on all topics from whole number operations to fractions to functions! Never be without a lesson again! Every lesson/example is fully illustrated. After all, this is a visual approach.

An idealized Teacher-Pupil dialogue is included in all lessons. If only the students would learn their part in the script! Key phrases in simple language are highlighted, giving the preferred verbalizations to transmit important math concepts. Actual student responses give experienced teachers the right track to run-on. A consistent approach gives clarity to the pattern employed with all examples in the curriculum. Every example includes the steps of Build it with manipulatives, Draw it to develop Visualization, do the Notation, and Record the answer. Specific lessons on teaching Notation, e.g. algorithms for operations, occur throughout. Also a chapter on the teaching of algorithms of notation and the significance of the relationship between them and the spatial reality of the constructions is included. The psychology of employing manipulatives is explained. In particular the value of the tactile motor-kinaesthetic experiences to learning mathematics is discussed. Order The Teacher's Handbook for Teaching Mathematics with Manipulatives right now, and I will include a 5-hour VHS videotape of my workshop covering the entire Mortensen method using three different sets of manipulatives, at no extra charge! This videotape of my workshop, videotaped at the University of Calgary, is a $99 value by itself. But I'll include it FREE if you order within 30 days. Imagine being able to reference lessons from the curriculum, including: all operations, problem solving, decimals, algebra, fractions - and being able to watch the lesson being taught by "Canada's resident expert on Mortensen Math" at the same time!

Special Offer!

Purchase The Teacher's Handbook for Teaching Math with Manipulatives right away by filling out the form below and mailing a cheque or by faxing the order with your visa, master charge information and receive a very special audiotape! Multiplication Facts are an undeniable foundation stone to learning math and the most enjoyable way of acquiring them is by means of songs and music. This audio tape of Jerry Mortensen himself playing keyboards and singing ten skip counting songs, which accompany his specially designed coloring books - very popular with younger learners, is a $10 value and I'll send it FREE if I receive your order within 30 days.

Yours sincerely,

Geoff White, B.Ed.

To Order:

The Teacher's Handbook for Teaching Math with Manipulatives

by Geoff White, B.Ed.

Only $79, plus $20 s&h - Paypal is preferred
e-mail me with order, I will e-invoice you for payment.

Order by Jan 31,2012 and receive, AT NO EXTRA CHARGE!
my 5 hour VHS workshop videotape (a $99 value) and the Special audiotape of Jerry Mortensen performing Skip Count Songs! (a $10 value) ABSOLUTELY FREE!

Act now!

Orders outside N.A. please inquire about S&H