Related Topics:
Psychological Principles of Learning re: Piaget
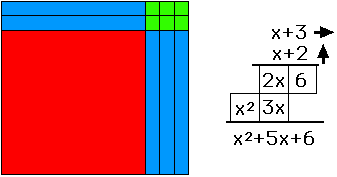
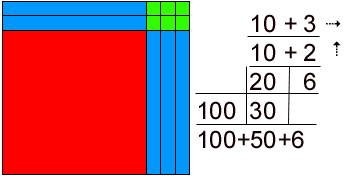
Explore and Discover1.) All you need to know is how to count to 9 and to build a rectangle 2.) One of the key principles of MM is "to see all numbers as rectangles." What does this mean? Traditionally when a speaker says "six" the listener has a mental image of the numeral 6. Yet, when a speaker says "Mike!" the listener sees Mike's face in her mind's eye. Similarly with other nouns like red apple, barn, Statue of Liberty, we form a mental image of the object as it is mentioned by name. We do not have a mental image of the name, as in block capital letters, say. We don't "see" B-A-R-N in our mind's eye, we see what that object looks like. A rectangle has area and dimension, two of them, Mortensen calls them the "over" and "up." Dimensions. 3.) All we do in math is count is another key principle. What do we do with numbers? Even the youngest child knows that: we count with them. To count you first must know what one is. See one as a rectangle that is "one over" and "one up" Now, all operations are just building rectangles and therefore all a child needs to know to do all the math there is, is to count to nine and to build a rectangle. As in all skill-learning, knowledge of results is important. When relying on memory to do math in the traditional way, there is no certainty, no way of knowing that you have done it right. With Mortensen Math there is a very good visual check. If the rectangle has no holes in it, and no bits sticking out, then it is correct. The learner can see that it is right. This builds confidence. Suppose Math could be used to build self-esteem, instead of robbing people of it? That is what Mortensen Math does. By using manipulatives in a manner that makes mathematics accessible to all, subordinating mere symbol manipulation to the role of notation, by using a universal, comprehensive system that enables students to build on their experiences Mortensen Math makes success in math available to all. Nothing builds confidence and self-esteem like success in mathematics. Mortensen Math is named for Jerry Mortensen, who designed the program after working for years in Montessori schools. The blocks are an adjunct to the method. That is to say this is a unique approach to teaching Mathematics that also employs manipulatives rather than that this is a manipulative method of teaching math as would be, say, teaching the use of an abacus. A few examples to begin with. Then we can look at how we arrived at this method an examine some of the psychological principles. Mortensen math is a highly visual approach. We use manipulatives in teaching every concept. There is so much to be gained by that manipulative experience it would be a mistake to teach only part of the math curriculum using manipulatives. We can employ manipulatives in teaching all topics in math from kindergarten to grade twelve and beyond. There is a complete set of exercise books written by Jerry Mortensen available covering the K-12 curriculum with accompanying manuals for the use of the teacher or parent in the case of homeschoolers. Mortensen has also designed three distinct sets of manipulatives based on the principles of the method. Mortensen owns several U.S. patents relating to the system. It requires minimal training of the instructor to use Mortensen Math. While unique in its approach the method can be adopted easily by any teacher and acquired without intense study. In fact this book and the accompanying video workshop is all that is necessary to facilitate the teaching of math with manipulatives using the Mortensen method. We will show you how you can develop analytical thinking skills and creative problem solving ability at an early age. We will show how using this method will enable all students to experience success with math. Success with math is the greatest motivator there is in the school system. Chances are that no child who failed high school also had high scores in mathematics. The child who experiences success in math will be motivated to do more. Success breeds more success. "Hey, I can do this. This feels good. I feel good about myself." Self-esteem rises. They want to do more. We use creative problem solving to develop critical thinking. In teaching mathematics what we really want to be doing is solving problems. We spend most of the first ten years of school life teaching the tools that we need to do the calculations necessary to derive the answers to problems before we expose students to story problems themselves around grade ten, which is part of the reason for the crunch that occurs at about that time for many students. The tragedy is that is about the time when they are given the option of dropping math or of taking a watered down math course aimed at some other vocation. We want to use the tools of long division or handling fractions to solve problems, whether they be in the farmer's field, taking advanced engineering courses or in the home, planning the budget, buying carpet or paint cooking or making clothes. Take an example of multiplication: 12 times 13. I have chosen this example because it is beyond the scope of times tables, which are usually taught up to 12 x 12. Let's see what it is to count 12 thirteen times. Let's put out some small unit blocks in groups of twelve until we have set out 13 groups of 12 on the table. When I've got that I will regroup them into tens and count those, and arrive at an answer. A familiar process. The first difficulty that might arise is that a unit block might be counted twice, first in one group, then in an adjacent group if the groups are not well separated spatially. The eye can be confused when counting quickly. So let us line them up. Then I can see that by adding the next group in line with the previous one, we are in fact building a rectangle. We can see that if no unit is out of alignment then that error is eliminated. So counting in this way becomes "building rectangles." Furthermore, if we are using base ten blocks, including ten bars and hundred squares along with the units, the child may discover that with suitably sized counting operations, by building the rectangle with larger pieces the counting job can be done much more easily and quickly. By placing two ten bars along side a hundred square it can be discovered that this is like counting 12 ten times. Adding three more rows of 12 completes the counting of 12 thirteen times. (see fig. 1 opposite) Counting is like building rectangles and building rectangles makes the counting faster and more accurate - because there are no holes or bits sticking out. If there are holes or bits sticking out, it isn't a rectangle. This visual check gives confidence to the student that they are getting it right, or succeeding. Now we have a pretty construction - a rectangle 12 in the over dimension and 13 in the up dimension. By separating the pieces between the natural divisions - between the tens and the units and the tens and the hundred - then shifting the rows until the pieces line up, like with like, - we can count generally what we have: one of those (hundred squares,) five of these (ten bars,) and six of those (unit cubes.) One - five - six. One hundred, fifty-six. My answer is obvious. Try this a few times by yourself, then with a child and watch for a reaction. If their face lights up in a smile - the lights go on, as it were, and they say, "Hey that's neat! I like that. I understand that." then you know you are onto something. That's the kind of result we want - the feelings of success. What we have to do is go right back to where the child begins to count. The following is an introduction given by Jerry Mortensen to an assemblage of Math teachers and school board members. I have given this same intro hundreds of times myself to groups of teachers or home schooling parents and always with the same enthusiastic response: This makes sense. Now we are getting somewhere. All we do in Math is Count. Building Rectangles makes the counting rapid and more accurate.
If learning math were fun how hard would it be to get the students to do their work?
|
So what do you need to start teaching math the Mortensen way?
Order The Teacher's Handbook
To order, E-Mail: geoff @ geoffwhite.ws or, just send $65 via Paypal to: geoff @geoffwhite.ws with your email The Handbook for Teaching Math with Manipulatives is 250 8.5x11 pages of detailed, illustrated - in full color,
easy-to-read instruction on employing the Mortensen method written by Canada's leading practitioner
of the method.
In an 8.5 by 11 inch format, it lays flat on the table for easy reference - no more spine-breaking
stiff texts that need to be weighted down for hands-free use.
Included are 200 pages of actual lessons on all topics from whole number operations to fractions
to functions! Never be without a lesson again!
Every lesson/example is fully illustrated. After all, this is a visual approach.
An idealized Teacher-Pupil dialogue is included in all lessons. If only the students would learn their part in the script! Key phrases in simple language are highlighted, giving the preferred verbalizations to transmit important math concepts. Actual student responses give experienced teachers the right track to run-on. A consistent approach gives clarity to the pattern employed with all examples in the curriculum. Every example includes the steps of Build it with manipulatives, Draw it to develop Visualization, do the Notation, and Record the answer. Specific lessons on teaching Notation, e.g. algorithms for operations, occur throughout. Also a chapter on the teaching of algorithms of notation and the significance of the relationship between them and the spatial reality of the constructions is included. The psychology of employing manipulatives is explained. In particular the value of the tactile motor-kinaesthetic experiences to learning mathematics is discussed. Order The Teacher's Handbook for Teaching Mathematics with Manipulatives right now, and I will include a 5-hour VHS videotape of my workshop covering the entire Mortensen method using three different sets of manipulatives, at no extra charge! This videotape of my workshop, videotaped at the University of Calgary, is a $99 value by itself.
But I'll include it FREE if you order within 30 days. Imagine being able to reference lessons from the
curriculum, including: all operations, problem solving, decimals, algebra, fractions - and being able
to watch the lesson being taught by "Canada's resident expert on Mortensen Math" at the same time!
Special Offer!
Special Offer!Order by July 31 and get a 5-hour VHS tape of my MM Workshop FREE! Pay by Paypal & receive a 60-minute "Skip Counting" audio tape FREE! shipping extra, add US$20 in N.A. (elsewhere by quote)
Order The Teacher's Handbook
E-Mail: geoff @ geoffwhite.ws Special Offer!Order by July 31, 2012 and get a 5-hour VHS tape of my MM Workshop FREE! Pay by Paypal & receive a 60-minute "Skip Counting" audio tape FREE! shipping extra, add US$20 in N.A. (elsewhere by quote) |
Geoff White, B.Ed.
To Order:
The Teacher's Handbook for Teaching Math with Manipulatives
by Geoff White, B.Ed.
Send $79 + $20 S&H by Paypal to
geoff @ geoffwhite.ws
Be careful to include all the correct shipping details
Order by July 31, 2012 and receive, AT NO EXTRA CHARGE! the 5 hour VHS workshop videotape (a $99 value) and the Special audiotape of Jerry Mortensen performing Skip Count Songs! (a $10 value) ABSOLUTELY FREE!
Act now!
Orders outside Canada please inquire re: shipping
| Purchasing Dilemmas | Products/Price List | Comparing Methods | Understanding | Mental Images | A Fractions Example | Psychological Principles at Work | Self-Esteem - Teacher's Role | Acquiring Meaning | A Philosophy of Teaching Math | A Math-Rich Environment | Main Page